Let's talk about syntax trees. In static analysis, a common operation is to take a character string (e.g. "x = 1") and transform it into well structured data:

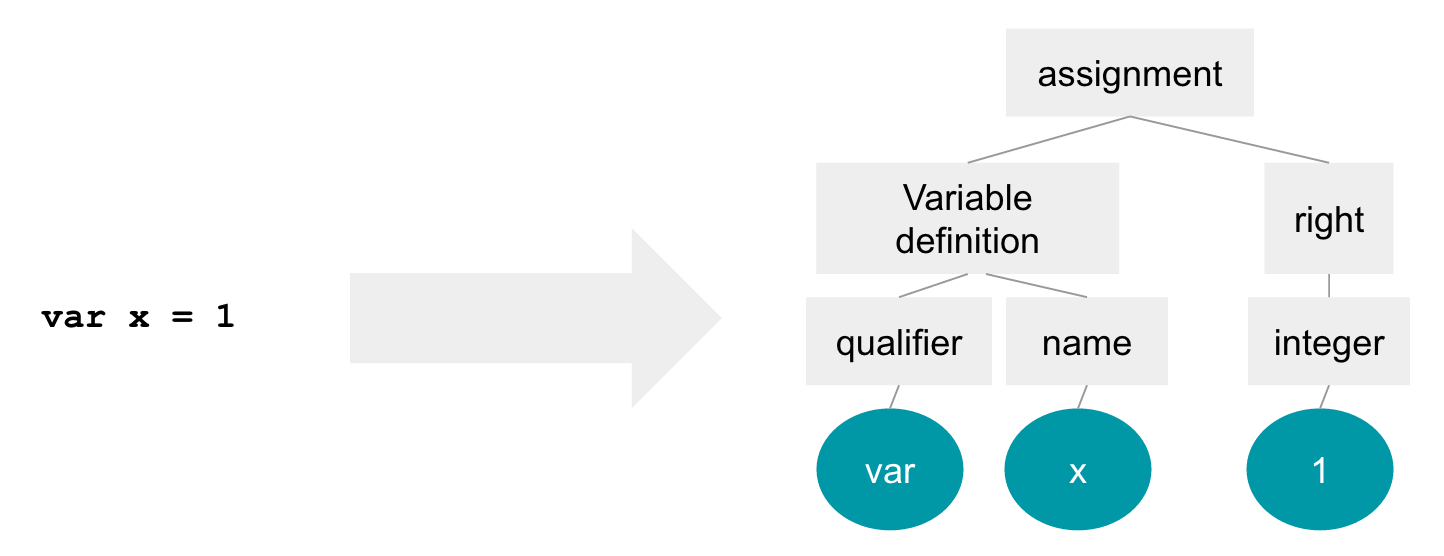
Let's try to do this in python. We'll use Pyparsing as our tokenization tool - you can use pyparsing's rules to build a grammar, from which you can get back a list of token data.

from pyparsing import alphas, Word, Literal, nums

grammar = Literal("var") + Word(alphas) + Literal("=") + Word(nums)

>>> print(grammar.parseString("var x = 1"))
['var', 'x', '=', '1']

This is great, but what if we need a tree instead of an array of tokens?

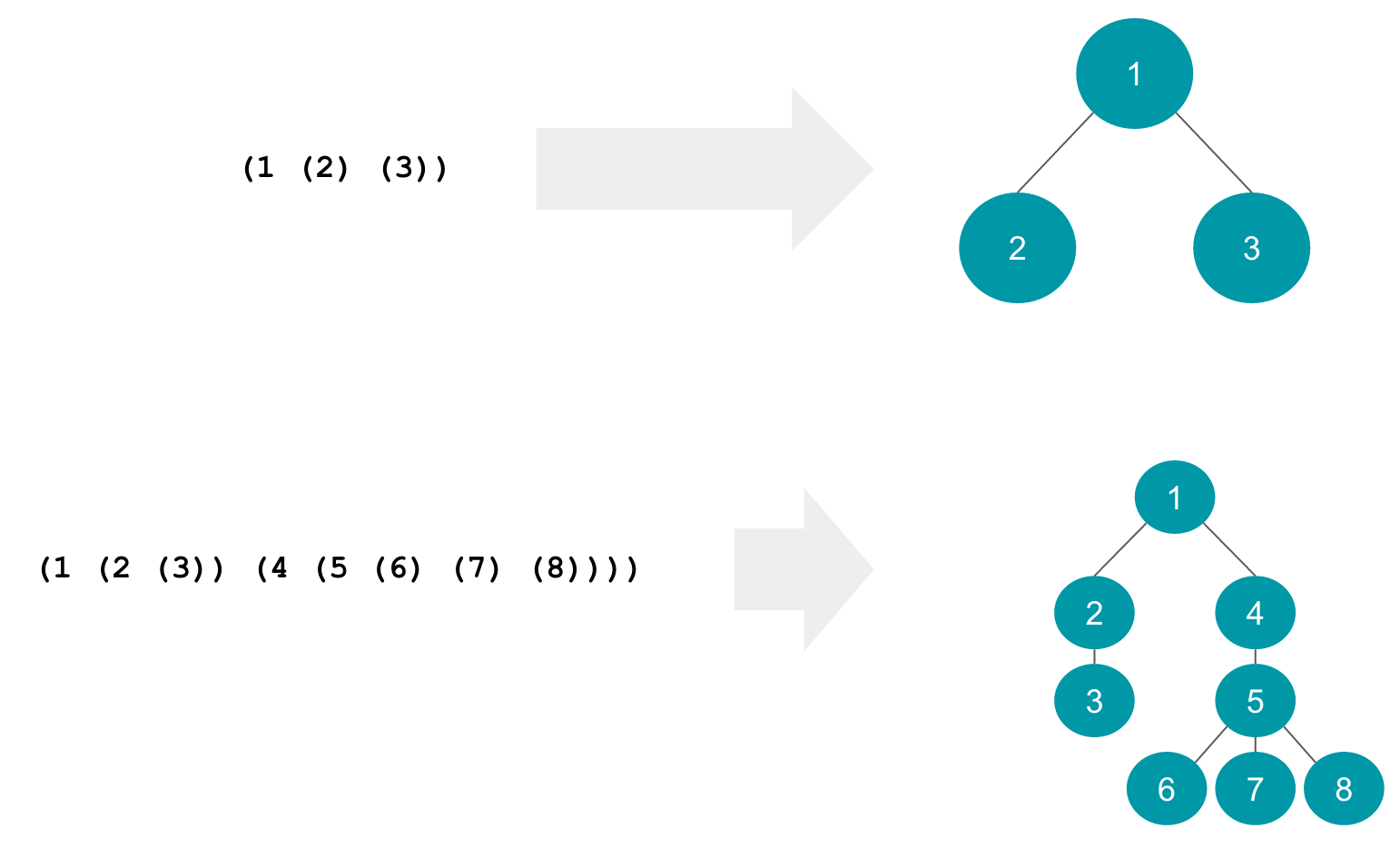
For example, let's say we have a language that describes a tree, where each node in the tree can have a number. Each node is represented by a pair of parentheses, and inside is the value followed by the child nodes:

How could we write a parser for this? It differs in a couple of ways from the first example:

1. It's inherently recursive, since after the value in each node, zero or more child nodes can follow:

   node := (value[, node, node, node, ...])
   

2. If we parse the string as a list, we won't be able to preserve the tree structure.

Recursive grammars with pyparsing

Pyparsing supports recursive grammars using a grammar component called Forward. To define a recursive grammar, you create a pyparsing.Forward(), then use the shift left operator to set its content:

grammar = pyparsing.Forward()
grammar << pyparsing.Suppress("(") + pyparsing.Word("0123456789") + pyparsing.ZeroOrMore(grammar) + pyparsing.Suppress(")")

query = "(1 (2 (3)) (4 (5 (6) (7) (8))))"

>>> print(grammar.parseString(query))
['1', '2', '3', '4', '5', '6', '7', '8']

This parses the grammar, but we still don't have the tree structure.

Parse actions

Pyparsing allows a "parse action" to be defined:

def action(string, location, tokens):
    return tokens

grammar.setParseAction(action)

The parse action is a function which will be applied every time a parse element generates output. It takes three arguments:

1. The full input string being parsed.
2. The location of the parse element as an index into the full string.
3. The list generated tokens, as strings.

The value returned from the parse action function will replace the string tokens, and the default implementation does nothing with the tokens and just returns them the way they are. The parse action is our chance to hook into pyparsing and output structured data instead of strings.

As an example:

import pyparsing

class Item:
    def __init__(self, value):
        self.value = value

    def __repr__(self):
        return "{Item: %s}" % self.value

def transform(string, location, tokens):
    return [Item(token) for token in tokens]

grammar = Literal("var") + Word(alphas) + Literal("=") + Word(nums)
grammar.setParseAction(transform)

>>> print(grammar.parseString("var x = 1"))
[{Item: var}, {Item: x}, {Item: =}, {Item: 1}]

Now we have items instead of strings.

Building a tree

Let's apply this to the tree grammar to build a tree. We'll define a simple node class:

from collections import namedtuple

Node = namedtuple("Node", ["value", "children"])

And define the recursive grammar:

from pyparsing import Forward, Suppress, Word, ZeroOrMore

grammar = Forward()
grammar << Suppress("(") + Word("0123456789") + ZeroOrMore(grammar) + Suppress(")")

def parseAction(string, location, tokens):
    return Node(value=tokens[0], children=tokens[1:])

grammar.setParseAction(parseAction)

And a way to print it out and see if it worked:

def pprint(node, tab=""):
    print(tab + u"┗━ " + str(node.value))
    for child in node.children:
        pprint(child, tab + "\t")

The result we are looking for is in the first item ([0]) of the parsing result.

>>> pprint(grammar.parseString("(1 (2 (3)) (4 (5 (6) (7) (8))))")[0])
┗━ 1
    ┗━ 2
        ┗━ 3
    ┗━ 4
        ┗━ 5
            ┗━ 6
            ┗━ 7
            ┗━ 8

Not bad: a simple parser in 9 lines of code.